繼 AI 將文字變成圖片后,又有 AI 可以將文字變成 3D 場景了。
蘋果發布新 AI 系統 GAUDI,能在室內生成 3D 場景
近日,蘋果 AI 團隊發布最新 AI 系統 GAUDI,GAUDI 基于用于生成沉浸式 3D 場景的神經架構 NeRFs,可以根據輸入的文字提示生成 3D 室內場景。
在此之前,OpenAI 的 DALL-E 2 以及谷歌的 Imagen 和 Parti 等 AI 系統都展示了將文字生成圖片的能力,但生成的內容僅限于 2D 圖像和圖形。
2021 年年末,谷歌通過 Dream Fields 首次展示了新的 AI 系統,該系統將 NeRF 生成 3D 視圖的能力與 OpenAI 的 CLIP 評估圖像內容的能力相結合。而蘋果 AI 團隊發布的 GAUDI 則更進一步,能夠生成沉浸式 3D 場景的神經架構,并可以根據文字提示創建 3D 場景。
例如,輸入“穿過走廊”或“上樓梯”,就可以看到執行這一動作的 3D 場景視頻。
據了解,NeRFs 是一種主要用于 3D 模型和 3D 場景的神經存儲介質,并能夠從不同的相機視角進行渲染。
此前,將生成 AI 擴展到完全不受約束的 3D 場景是一個尚未解決的問題。這背后的原因之一是受限于攝像機位置:雖然對于單個對象,每個攝像機位置都可以映射到一個圓頂,但在 3D 場景中,這些攝像機位置會受到對象和墻壁等障礙物的限制。
對于這個難題,GAUDI 模型的解決方案是:相機姿態解碼器對可能的相機位置進行預測,并確保輸出是 3D 場景架構的有效位置。
雖然當前 GAUDI 生成的 3D 場景視頻質量很低,但這也預示了 AI 在未來新的可能,或許在 AI 的下一階段,我們可以看到更多驚喜。
GAUDI 背后的技術實現
根據蘋果方面的介紹,GAUDI 的目標是給定 3D 場景軌跡的經驗分布時,學習得出生成模型。
論文地址:
https://arxiv.org/pdf/2207.13751.pdf
具體技術實現方面,令 X = {xi∈{0,…,n}}表示所定義的經驗分布示例集合,其中每個示例 xi 代表一條軌跡。每條軌跡 xi 被定義為相應的 RGB、深度圖像與 6DOF 相機位姿的可變長度序列。
蘋果 AI 團隊將學習生成模型這個任務拆分成兩個階段。首先,為每個示例 x ∈ X 獲取一個潛在表示 z = [zscene, zpose],用于表達場景輻射場和在單獨的解糾纏向量中的位姿。接下來,給定一組潛在的 Z = {zi∈{0,...,n}},目的就是學習分布 p(Z)。
1.優化輻射場與相機姿勢的潛在表示
為每個示例 x ∈ X(即經驗分布中的每條軌跡)尋找潛在表示 z ∈ Z。為了獲得這一潛在表示,團隊采用了無編碼器視圖,并將 z 解釋為通過優化問題[2,35]找到的自由參數。為了將潛在 z 映射至軌跡 x,我們設計了一套網絡架構(即解碼器),可用于解析相機姿勢與輻射場參數。這里的解碼器架構由 3 個網絡構成(如下圖所示):
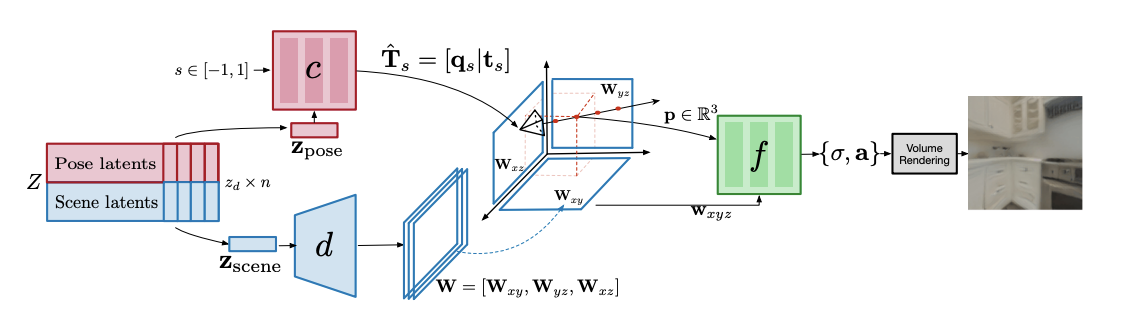
負責將相機位姿與 3D 幾何及場景外觀分離的解碼器模型架構。解碼器包含三個子模塊:解碼器 d 將用于表示場景 zscene 的潛在代碼作為輸入,并通過三平面潛在編碼 w 生成 3D 空間的分解表示。輻射場網絡 f 則將 p ∈ R3 作為輸入點,并以 W 為條件通過體積渲染(方程 1)預測出密度σ和信號 a。最后,我們通過網絡 c 解碼相機位姿。網絡 c 將歸一化的時間位置 s ∈ [-1, 1]作為輸入,并以 zpose(表示整個軌跡 x 中的相機位姿)為條件,預測出相機位姿 T^ s ∈ SE(3)。
相機位姿解碼器網絡 c(由θc 實現參數化)負責預測軌跡中歸一化時間位置 s ∈ [-1, 1]處的相機位姿 T^ s ∈ SE(3),其中的 zpose 條件則代表整個軌跡的相機位姿。為了確保 c 的輸出為有效相機位姿(例如 SE(3)的一個元素),輸出一個 3D 向量,用以表示方向的歸一化四元數 qs 外加 3D 平移向量 ts。
場景解碼器網絡 d(由θd 實現參數化)負責預測輻射場網絡 f 的條件變量。該網絡將表示場景 zscene 的潛在代碼作為輸入,可預測出以軸對齊的三平面表示[37, 4] W ∈ R 3×S×S×F。與空間維度 S x S 和 F 通道的三個特征圖[Wxy,Wxz,Wyz]相對應,每個軸分別對齊一個平面:xy、xz 與 yz。
輻射場解碼器網絡 f(由θf 實現參數化)的作用,是使用方程 1 中的體積渲染議程重建圖像級目標。其中 f 的輸入為 p ∈ R 3 和三平面表示 W = [Wxy,Wxz,Wyz]。給定一個要預測輻射度的 3D 點 p = [i, j, k],將 p 正交投影至 W 中的每個平面,并執行雙線性采樣。將這 3 個雙線性采樣向量連接成 wxyz = [Wxy(i, j),Wxz(j, k),Wyz(i, k)] ∈ R 3F,用于調節輻射場函數 f。這里,蘋果 AI 團隊將 f 實現為輸出密度值σ和信號 a 的 MLP。為了預測像素的值 v,使用體積渲染議程(參見方程 1),其中的 3D 點表示特定深度 u 處的光線方向 r(相對于像素位置)。
方程1
團隊還確立了去噪重建目標,用以聯合優化θd, θc, θf 和{z}i={0,...,n},詳見方程 2。
請注意,雖然潛在 z 是針對每個示例 x 獨立優化的,但網絡θd, θc, θf 的參數由所有示例 x ∈ X 均攤。與之前的自動解碼方法[2,35]不同,每個潛在 z 在訓練過程中都會受到與所有潛在模型的經驗標準差成正比的加性噪聲干擾,即 z = z+βN (0,std(Z)),從而導致收縮表示[46]。在這種情況下,β控制分布 z ∈ Z 的熵與重建項間的權衡:當β= 0 時,z 的分布為指示函數的集合;而β > 0 時,潛在空間則為非平凡結構(non-trivial structure)。使用一個較小的β > 0 值強制獲得一個潛在空間,插值樣本(或包含與經驗分布具有小偏差的樣本,即可能從采樣后續生成模型中獲得的樣本)將受解碼器支持以被包含其中。
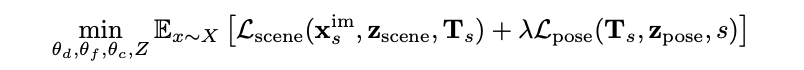
方程2
使用兩種不同的損失函數對參數θd, θf , θc 和潛在變量 z ∈ Z 進行優化。第一個損失函數 Lscene 負責測量在 zscene 中編碼的輻射場與軌跡 x im s 中的圖像之間的重建(其中 s 表示幀在軌跡中所處的歸一化時間位置),這時需要給定實際相機位姿 Ts。
對 RGB 使用 l2 損失函數,對 4 depth 1 使用 l1 損失函數。第二個損失函數 Lpose 則測量在 zpose 中編碼的位姿 T^ s 與真實位姿之間的相機位姿重建差。對平移使用 l2 損失,對相機位姿的歸一化四元數部分采用 l1 損失。盡管在理論上,歸一化四元數并不一定唯一(例如 q 和-q),但在訓練期間并未發現任何經驗問題。
2.預先學習
給定一組潛在的 z ∈ Z,這些 z 由對方程 2 中目標的最小化產生。目的是通過學習獲得一個生成模型 p(Z),并捕捉其分布(即在最小化方程 2 的目標之后,將 z ∈ Z 解釋為潛在空間中經驗分布的形式)。為了對 p(Z)進行建模,團隊采用了去噪擴散概率模型(DDPM)[15],這是一種新近出現、基于分數匹配[16]的模型。該模型能夠通過大量但有限的時間步數,學習馬爾可夫鏈的逆向擴散。
DDPMs 表明,這一逆向過程等效于學習一系列具有綁定權重的去噪自動解碼器。DDPM 中的監督去噪目標使得學習這(Z)變得簡單且可擴展。由此,我們就能學習得到一個強大的生成模型,該模型能夠以無條件/有條件方式生成 3D 場景。為了訓練先前的 pθp (Z),采用方程 3 中定義的目標函數。在方程 3 中,t 代表時間步長,~ N (0, I)為噪聲,αˉt 為具有固定調度的噪聲幅度參數,θp 則表示去噪模型。
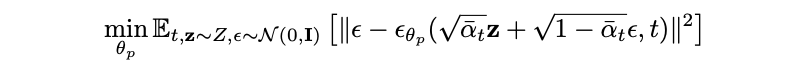
方程3
在推理期間,團隊會遵循 DDPM 中的推理過程以對 z ~ pθp (Z)進行采樣。首先對 zT ~ N (0, I)采樣,之后迭代應用θp 對 zT 進行梯度去噪,從而逆向擴散馬爾可夫鏈以獲得 z0。接下來,將 z0 作為輸入提供給解碼器架構,借此重建輻射場和相機路徑。如果目標是學習潛在變量 p(Z|Y )的條件分布,則應給定配對數據{z ∈ Z, y ∈ Y },為去噪模型θ增加一個條件變量 y,由此得到θp (z, t, y)。

